Przewrót kopernikański – fizyka kwantowa przychodzi z pomocą
Oczekujemy przewrotu kopernikańskiego w informatyce. Zmiany podejścia. Wyjścia poza uznane standardy i status quo. Thomas Kuhn w książce The Structure of Scientific Revolutions opisał to zjawisko nazwane przez niego „paradigm shift”, czyli w wolnym tłumaczeniu właśnie zmiana podejścia.
Polecam wszystkim tę książkę, która mimo tego, że powstała w 1962 roku opisuje zjawiska, które obowiązują w nauce i technologii po dziś dzień. Jedną z jego obserwacji było właśnie „paradigm shift”. Według autora, przełomy w tych dziedzinach zwykle nie odbywają się stopniowo, krok po kroku, a gwałtownie, szybko i spektakularnie. Tak było po wymyśleniu silnika parowego, tranzystora czy technologii cyfrowej. Całkowita zmiana sposobu myślenia.
Procesory krzemowe wykonujące liniowe rozkazy na zerach i jedynkach mają swoje ograniczenia i prędzej czy później ich wydajność niemalże się zatrzyma. Ale nie jest to jedynie melodia przyszłości. Już teraz klasyczne komputery nie radzą sobie z wieloma zagadnieniami. Istnieje cała klasa problemów zbyt złożonych obliczeniowo dla współczesnych maszyn liczących. Klasę tę nazwano NP (w tym problemy NP-zupełne i NP-trudne). NP, czyli problemy niedeterministycznie wielomianowe. Brzmi strasznie, prawda? Nie zagłębiając się jednak w matematyczne podstawy, jest to problem decyzyjny, dla którego rozwiązania nie można zweryfikować w czasie wielomianowym (czytaj: jego rozwiązanie będzie trwać baaaaaaardzo długo). Wraz ze wzrostem wymiarowości (skali) problemu czas potrzebny na rozwiązanie gwałtownie rośnie i może wielokrotnie przekroczyć… wiek wszechświata.

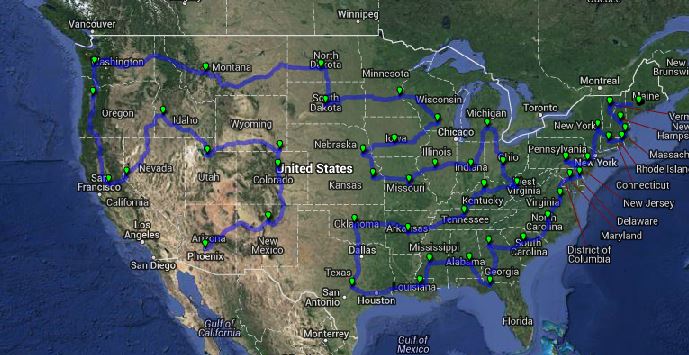
Dalej nie brzmi to zbyt jasno. Posłużmy się zatem przykładem. Jednym z najpopularniejszych problemów NP jest tak zwany problem komiwojażera. Jeśli sięgniemy do definicji, znowu natkniemy się na matematyczną nowomowę – „jest to zadanie optymalizacyjne polegające na znalezieniu minimalnego cyklu Hamiltona w pełnym grafie ważonym”. Nazwa pochodzi od zobrazowania tego zagadnienia, przedstawiającego problem z punktu widzenia wędrownego sprzedawcy – wyznaczone jest „n” miast, które komiwojażer ma odwiedzić, oraz odległość pomiędzy każdą parą miast (graf ważony). Rozwiązaniem problemu komiwojażera jest znalezienie najkrótszej drogi łączącej wszystkie miasta zaczynającej się i kończącej się w określonym punkcie.
Brzmi banalnie, prawda? Poza tym, po co komuś takie czysto teoretyczne rozważania? No ok, przypomina to trochę znajdowanie najkrótszej drogi przez aplikacje nawigacji, z których korzystamy na co dzień. Zajmuje to zaledwie kilka sekund, w czym zatem problem? W tym, że algorytmy zakodowane w naszych nawigacjach nie znajdują trasy optymalnej. A mówiąc bardziej precyzyjnie: trasa którą wyznaczają NIE MUSI być optymalna. Korzystają one z tzw. algorytmów zachłannych („greedy”), czyli takich które w celu wyznaczenia rozwiązania w każdym kroku dokonują „zachłannego” (najlepiej rokującego w danym momencie) wyboru rozwiązania częściowego. Mówiąc prościej – algorytm zachłanny nie dokonuje oceny czy w kolejnych krokach jest sens wykonywać dane działanie w skali globalnej, a dokonuje on wyboru WYDAJĄCEGO się w danej chwili najlepszym. Przykład? Wyznaczając trasę Warszawa – Paryż, algorytm zachłanny nie analizuje wszystkich możliwych tras (jest to problem NP, którego analiza zajęłaby miliardy lat), a jedynie kolejne pozornie optymalne kroki. I tak pierwszym krokiem byłoby na przykład przeanalizowanie czy opłaca się jechać przez Poznań, Kraków czy Gdańsk. Lokalnie optymalnym rozwiązaniem będzie Poznań. Dzięki temu problem sprowadza się do znalezienia (krótszej) trasy Poznań – Paryż. I tak w kilku (kilkudziesięciu? kilkuset?) krokach otrzymujemy rozwiązanie. Nie mamy jednak pewności, że jest to trasa optymalna, gdyż algorytm nie przeanalizował wszystkich możliwych tras. Podsumowując – dla zadań dużej skali (wymiarowości) nie jest możliwe przeanalizowanie w sensownym czasie wszystkich kombinacji rozwiązań (problem NP), stosuje się zatem algorytmy „zachłanne” które mniej lub bardziej skutecznie potrafią zbliżyć się do rozwiązania optymalnego. Ale nie zawsze je znajdują.
Kolejnym praktycznym zastosowaniem problemów NP i ograniczeń klasycznych komputerów jest szyfrowanie oparte na faktoryzacji liczb będących iloczynem dwóch liczb pierwszych. Faktoryzacja to po prostu rozkład na czynniki. Chcąc rozłożyć na czynniki liczbę 6, otrzymamy 3 i 2 (parę liczb pierwszych). Każda liczba, która nie jest liczbą pierwszą składa się z iloczynu co najmniej dwóch liczb pierwszych. RSA to jeden z pionierskich asymetrycznych (z kluczem publicznym i prywatnym) algorytmów kryptograficznych. Jego siła szyfrowania opiera się właśnie na trudności faktoryzacji dużych liczb złożonych (pary losowo wybranych dużych liczb pierwszych). Po informacje czym jest klucz publiczny i prywatny i jak się je generuje odsyłam do Wikipedii, ale wróćmy do zagadnienia rozkładu liczby na czynniki i trudności z tym związanych. W Internecie znajdziemy prosty przykład: mając dwie liczby 65537 i 65539, można szybko je pomnożyć przez siebie i w ułamkach sekund otrzymać wynik: 4295229443. Jednak rozłożenie 4295229443 na czynniki jest trudne – rozłożenie czyli znalezienie tych dwóch liczb będących dwoma czynnikami działania mnożenia. Faktoryzacja odpowiednio długiej liczby zajmie współczesnym komputerom miliony lub miliardy lat (w zależności od długości wybranej liczby).
Ale jaki to ma związek ze zmianą paradygmatu? Zasadniczy. Jeśli nie zmienimy podejścia, współczesne komputery, mimo ciągłego zwiększania mocy obliczeniowej i tak nigdy nie poradzą sobie ze złożonymi problemami klasy NP. Z pomocą mogą nam przyjść… komputery kwantowe, które jeszcze niedawno były tylko abstrakcyjnym tworem w głowach fizyków. Musimy zacząć od definicji. Wikipedia podaje, że komputer kwantowy to układ fizyczny, do opisu którego wymagana jest mechanika kwantowa, zaprojektowany tak, aby wynik ewolucji tego układu reprezentował rozwiązanie określonego problemu obliczeniowego. Ciężko wyobrazić sobie gorszą definicję.
Zacznijmy zatem od początku. W klasycznych komputerach dane są jednoznacznie reprezentowane przez zera lub jedynki w kolejnych bitach pamięci. Na tych danych procesory wykonują operacje arytmetyczno-logiczne. Dane w komputerach kwantowych z kolei, reprezentowane są przez aktualny „stan kwantowy” komputera. Zmiany tego stanu odpowiadają procesowi obliczeniowemu. Najważniejsze jest to, że odpowiednie zaplanowanie tych zmian, czyli stworzenie celowego algorytmu kwantowego pozwalałoby na osiągnięcie wyników obliczeń w znacznie szybszy i wydajniejszy sposób, niż za pomocą komputerów klasycznych. Nadal jednak nie wiemy o co tak naprawdę chodzi.
Najważniejszymi elementami kwantowego komputera są kwantowe bramki logiczne. Kwantowy bit (kubit, qbit), zgodnie fizyką kwantową nie będzie miał ustalonej jednoznacznej wartości 1 lub 0. W trakcie wykonywania obliczeń będzie się znajdował w stanie pośrednim – kubit jest zatem kwantową superpozycją zera i jedynki. Pojedynczy wynik obliczeń komputera kwantowego będzie w związku z tym obarczony niepewnością. Istotne staje się więc wykonanie całej serii obliczeń i dopiero ich uśredniona wartość określi wynik (tym dokładniejszy, im więcej komputer dokona obliczeń).
Na temat podstaw teoretycznych można by napisać wiele więcej i poprzednie akapity jedynie w bardzo ogólny sposób objaśniają ten trudny temat. Posłużmy się jednak przykładem i wróćmy do problemu komiwojażera. Chcąc sprawdzić wszystkie możliwe drogi i wybrać najkrótszą, klasyczny komputer musiałby zapisać każdą z nich (z dróg) w postaci ciągu zer i jedynek (ciągu o tej samej długości dla każdej z tras), a potem na tej podstawie dla każdego ciągu dokonać obliczeń długości trasy. Liczba tych ciągów jest jednak tak ogromna, że nie starczyłoby ani pamięci ani mocy obliczeniowej, żeby wyliczyć to w skończonym (rozsądnym) czasie. Komputer kwantowy natomiast, zamiast kwantyliona różnych ciągów zer i jedynek (bitów) reprezentujących wszystkie możliwe trasy posłużyłby się jednym ciągiem kubitów i znalazł optymalny wynik w mgnieniu oka. Oczywiście przykład ten to duże uproszczenie, ale pozwala wyobrazić sobie dlaczego komputery kwantowe budzą tak wiele emocji i nadziei.


